 I was recently contacted by a former colleague, Dawn, regarding what manipulatives a grade one classroom might need to have on hand to support effective learning math. It seems a friend of Dawn’s is in a classroom which really has nothing for the children to use for hands-on math learning and they were wondering what was needed.
I was recently contacted by a former colleague, Dawn, regarding what manipulatives a grade one classroom might need to have on hand to support effective learning math. It seems a friend of Dawn’s is in a classroom which really has nothing for the children to use for hands-on math learning and they were wondering what was needed.
First off the classroom needs counters — counters in different shapes, sizes, etc. They can be purchased ones (such as mini plastic teddy bears) or ones gathered from home (such as bread tags, but†ons, etc.). But the need to be abundant and available.
Students need a way to count efficiently, especially in tens and ones. Egg cartons cut down to 10 holes, blank 10-frames printed on paper or card stock, or commercially produced 10-frames can all be used. I even like using cookie sheets (non-aluminum) and marking them with coloured tape as a giant 10-frame for use with magnets.
Base 10 blocks are also great for young students. These a generally in the form of small 1 cm cubes for “ones”, sticks for the “tens”, and flats for the “100’s”. I do want to make a critical point here: students may be engaged in a game of trading 10 cubes for a stick, or 10 sticks for a flat with every appearance of understanding the “ten-ness” of our base-10 number system. But be careful here. Student can be following your rule of trading 10 for 1 without that understanding. They might be just as happy to trade 8 for 1 or 12 for 1. The manipulatives give a opportunity for students to develop that important base-10 understanding, but moving blocks around correctly does not necessarily indicate that the understanding has been built in the student’s mind.
I think a grade one classroom needs “pop cubes” (multi-link cubes) — those blocks about 1inch in each dimension that can be attached together. I like to store them sticks of 5. If students need a particular amount for an activity, say 18, we discuss how many sticks each student will need, and then go get them. I also use these in many quick number-sense building activities. If I have students hold up a certain number of blocks, I want them to do so to model a ten frame. If I ask for 9 blocks and a student were to hold up a single stick of 9, I, as the teacher, cannot tell from a distance if the student is holding 8, 9, 10, or 11 blocks. But if he holds up a five stick beside a four stick, I can tell at a glance that he has the correct number. Pop cubes can be used in a multitude of math activities and should be on-hand for regular use.
Another must-have in my book are pattern blocks. They are particularly great for patterning activities for exploring symmetry, not to mention the creativity factor! I love them!
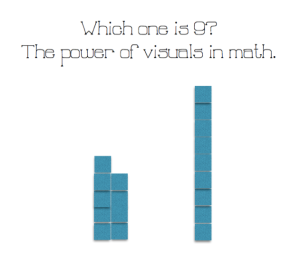
There are a number of things that I think should be in the classroom that are “make-able” such as dot cards, dot plates, printed ten-frames, even printed dominoes (click for more info on these)— all useful in exploring numbers, in building number sense, and in helping students develop the skill of subtilizing. Students need to SEE the numbers in math, and these materials can help develop that “seeing” in the children.
Of course there are many other things that are fun to have in the math classroom, such as dice, dominoes, blocks, playing cards, geoboards, plastic coins, bingo chips, square tiles, Cuisenaire rods, and two-colour counters, to name a few. But lots of math learning can take place with some thoughtfully crafted lessons and activities and just the basics.
I hope you will focus on the math understanding with whatever materials you have at your disposal!
Mathematically yours,
Carollee
 I am delighted to be here in Richmond, BC, today presenting at the BCTF’s New Teachers’ Conference. I am doing a similar workshop to what I did at the Calgary City Teachers’ Convention two weeks ago, but it is well worth the repeat in this city!
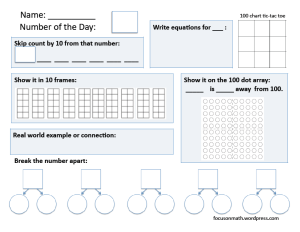
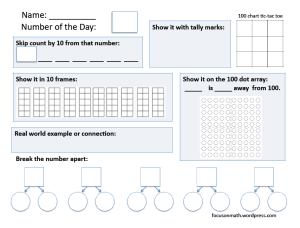
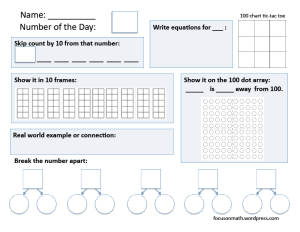
I am delighted to be here in Richmond, BC, today presenting at the BCTF’s New Teachers’ Conference. I am doing a similar workshop to what I did at the Calgary City Teachers’ Convention two weeks ago, but it is well worth the repeat in this city! The 100 Dot Array remains one of my favourite tools for helping students visualize numbers. This session at the CCTC focuses mainly on its use with students in grades 2 and 3, although it can be used at many other grade levels. We will be talking about the best way to introduce the tool to students, showing an early activity to help with general number sense, and using the number in problem solving situations. A variety of problem are included to show its diverse use.
The 100 Dot Array remains one of my favourite tools for helping students visualize numbers. This session at the CCTC focuses mainly on its use with students in grades 2 and 3, although it can be used at many other grade levels. We will be talking about the best way to introduce the tool to students, showing an early activity to help with general number sense, and using the number in problem solving situations. A variety of problem are included to show its diverse use.