Tessellations: Fun with Shape and Space May 31, 2013

Tessellations are a fun way to play with shape and space, a strand in the mathematics curriculum. A tessellation is a shape or combination of shapes which cover a two-dimensional surface without leaving any gaps. For example, square or rectangular tiles, common in houses, do this nicely, as do other shapes such as equilateral triangles, right triangles, and regular hexagons.

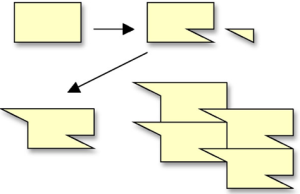
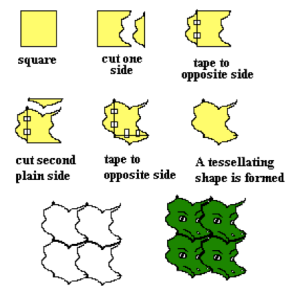
It is easy to create an interesting shape that tessellates by altering a shape that already tessellates. The important thing is to cut out a chunk of the tessellating piece, and then reattach it in such a way that the new altered shape will still be able to tessellate (see illustrations below for possiblilites).

I can hardly think about tessellations without thinking of the work by the Dutch artist M.C. Escher who did some amazing work in tessellations. This is a picture of one of his paintings called “Two Birds”. Check out this link to look at more of Escher’s work in this area.

Creating tessellations is a great activity for home or classroom, and even the most reluctant artist can create unique and wonderful pictures in this way. Thanks to Miss Norris for allowing me to post her students’ examples. Tessellations make a great math bulletin board!

I hope you will give tessellations a try!
Mathematically yours,
Carollee

Math Bulletin Board: Square Number Towers May 23, 2013

Recently I had two of my classes represent visually the idea of “squaring” a number: namely, that a number times itself is literally the area of a square with side length of that beginning number. The students cut squares from centimetre grid paper representing 10 x 10, 9 x 9, … 1 x 1 and them glued them onto construction paper. To each square they added the multiplication fact represented, as well as showing the exponential form of the number. Square numbers show up quite a bit in secondary mathematics, and helping students understand these numbers (as well as memorizing the sequence of them!) is beneficial for them as they move on.

I am always looking for math ideas to display on a bulletin board, and I think this is a good one!
Mathematically yours,
Carollee

Hat Tricks: Logical Thinking with Shadowchild May 21, 2013

Anno’s Hat Tricks (by Akihiro Nozaki and Mitsumasa Anno) is a wonderful way to introduce children to the realm of logic and the powerful word “if”. The book goes through a series of “tricks”, all of which can be solved by applying that “mathemagical” word “if”– a word that opens doors to new ideas. Children are introduced to the concept of using “if” statements to test the truth of an idea or supposition in a logical way. The reasoning pattern of “if…then” can be very useful, and, indeed, branches of modern mathematics have been developed by applying the word “if”.

This delightful book is mainly about three children: Hannah, Tom (both of whom are clearly seen) and Shadowchild (who exists on the page only as a shadow). The writer gives a series of scenarios in which the reader is shown a certain number of hats (all either red or white) which are available, and then which ones of those hats are being worn by Tom and Hannah. We are to use logic to deduce what colour hat Shadowchild is wearing. Although the first number of scenarios in the story are quite easy, the difficulty level increases throughout the book, with the final trick being the most difficult. (If you are not sure of your own level of logical thinking, there are several pages at the end of the book devoted to parents and other older readers that will offer some assistance in the logic being applied in the different tricks.)

Sadly, I think the book is no longer in print, but it is well-worth your while to track down a copy. I know and your children will enjoy the challenges presented.
Mathematically yours,
Carollee

History of Math to Archemedes (Video) May 3, 2013

This interesting video was posted yesterday on the BC Association of Mathematics Teachers’ (BCAMT) list serve (thanks Kelvin Dueck) and I thought I would post it here on the blog. It begins with the earliest discovery of “math” and moves quickly through some of the major developments in mathematics through the time of Archimedes. It touches on base 60 (Babylonians & Sumarians), early approximations of pi, simple fractions (from the Egyptians), square roots, magic squares, the Pythagorean theorem, prime numbers , the Fundamental Theorem of Arithmetic or prime factorization, using the the sieve of Eratosthenes to find smaller prime numbers. Maybe some of the ideas will be “Greek” to you, but then again, maybe it will spark a bit of curiosity, too!

Mathematically yours,
Carollee

Math Thinking with SD#60 Learning Assistants May 2, 2013

I just finished a session with the teachers who work as learning assistants in SD#60. We had a great morning talking about how to help make math meaningful to students who are struggling. And it really all comes down to meaning. Caine & Caine (1994) report “The brain “resists having meaninglessness imposed on it. By meaninglessness we mean isolated pieces of information unrelated to what makes sense to a particular learner.”

Oh, how sad that so many students go through days, weeks, months, and even years of mathematics in school without making meaning! There are so many great tools and ideas for building meaning and making the connections that develop understanding! If a child is not “getting it” in some area of math, we need to go back in the conceptual development of the topic to the point where there IS meaning and then build from there.

What are you doing today to build meaning in mathematics with your students (or your own children?)
Mathematically yours,
Carollee