Happy Pi Day Everyone! March 14, 2014

 π is one of the most widely-known mathematical constants both inside and outside the mathematics/scientific community and it has been around for a very long time!

The ratio of the circumference to the diameter of a circle is constant (namely, pi) and has been recognized for as long as we have written records.

A ratio of 3:1 appears in the following biblical verse: “And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it about.”  (I Kings 7, 23; II Chronicles 4, 2.)

The ancient Babylonians generally calculated the area of a circle by taking 3 times the square of its radius (=3), but one Old Babylonian tablet (from ca. 1900-1680 BC) indicates a value of 3.125 for pi.

π is commonly defined as the ratio of a circle‘s circumference C to its diameter d.

The ratio C/d is constant, regardless of the circle’s size. For example, if a circle has twice the diameter of another circle it will also have twice the circumference, preserving the ratio C/d.

Of course, there is humor in math, so here’s the joke of the day:

What is the official animal of Pi Day? Why, the pi-thon, of course!

Mathematically yours on the “mathy” day,

Carollee

 
 

Number of the Day – Level III March 10, 2014

Today I am posting the third Number of the Day sheet. I cannot overstate that I believe that elementary school students should be involved with numbers everyday they are in school!

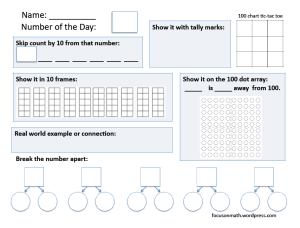
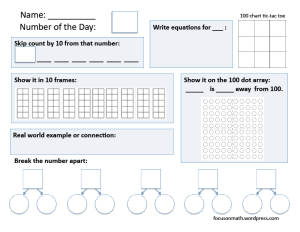
Level III is one to primarily use with numbers to 100. The section “100 chart tic-tac-toe” will not be familiar to most. I had devised that math game based on the positioning of a number on the 100 chart. For instance, if 26 is written in the centre of the chart, then the middle line is to show one more and one less than 26. (25, 26, 27 across). Above the middle number is 10 less, in this case 16. Below 26 is 10 more, 36 in this case. The corners can then be filled in using the horizontal or vertical relationships already established. (For more on the use of 100 chart tic-tac-toe, see my previous blog post.)

When using 100 dot arrays, I have students use highlighters to colour the numbers. I also stress marking efficiently – we do NOT colour each individual dot; rather a line or partial line is coloured with a swipe of the marker.

At every level breaking apart the number of the day is an important component of the sheet. Quoting John Van de Walle once again, “To conceptualize a number as being made up of two or more parts is the most important relationship that can be developed about numbers.” [Van de Walle, J. and Folk, S. (2005). Elementary and Middle School Mathematics: Teaching Developmentally (Canadian Edition). Pearson: Toronto.]

I did have one teacher ask a question about the breaking apart section. She was used to having students only break apart numbers according to tens and ones. Thus 26 could be broken apart as 20 and 6 or 10 and 16. But sometimes it is easier to work with numbers when we break them in ways other than ten and ones. Consider the thinking that might happen when adding 26 + 27. If a student knows that 26 comes apart as 25 an 1 and that 27 comes apart as 25 and 2, it is easy to put the 25′s together to get 50, then add the 1 and the 2 —total 53. Students who use the 100 dot array often get especially comfortable with 25′s. Also consider adding 97 and 36. If a student notices that 97 is just 3 away from 100, it makes sense to split 36 as 3 and 33. Breakng apart in tens and ones are definitely useful, but so are other “break-aparts”. If students do not practice this kind of thinking they are not likely to ever do it!

I had one teacher here in my district that was using this sheet and her students were getting tired of making tallies for large numbers. So I am including a second English version of the sheet asking for equations for the number instead.

Again, a French version is offered as well with thanks to my friend and colleague Lynn St. Louis for her translation.

 Download the English version (tallies) here.

Download the English version (equations) here.

Download the French version here.

Mathematically yours,

Carollee

Host a Parent Night in Math March 9, 2014

As I have worked with teachers both in this district and in other districts regarding changing their math practice, there is often another element that needs to be addressed. Parents of the students in the class begin to wonder and ask questions about how things are being done in the classroom. Parents notice that instead of a page of problems all done using the exact same “formula” or algorithm, a lesson may be structured quite differently, possibly around a single question! It seems so foreign and strange, and parents cannot help but ask, “What’s going on in math? Why does it look different than when we went to school? The other method worked for me – why, I passed math, so shouldn’t things just stay the same?”

One of things I do to support both teachers AND parents is to hold a “Math Night” for the parents of a given class or school. This is NOT meant to be a fun “Family Math Night” that is set up like a carnival with a variety of stations, all with activities centered on math topics. Those are wonderful events and can be an exciting way to expose parents and children to many interesting components in math, and they certainly have their place. I would encourage any class or school to host such an event!

However, there is a need to actually address mathematical issues with parents, so I am talking about a parent meeting that is meant to be something deeper, something to challenge the “why?” of how we have long taught mathematics. Such a meeting is meant to invite parents to think about what it means to “do math” and why it is “better to do one problem five ways than five problems one way” (Polya). I am asking parents to challenge the notion that just because they were taught a certain way does not make it an effective method of teaching.

Knowing that we are all busy, I keep the time frame to a minimum, but I usually plan for about an hour.

My Math Night plan looks something like this:

• Welcome and other necessary starting info (e.g., washrooms for young children)
• Introduction of me – who I am and how I am involved with the class/school/district (done either by the teacher/principal hosting the meeting or by me). If you are hosting for the parents of your own students, this step is, of course, unnecessary!
• Posing a problem: how many ways can we find to solve a problem
  • Doing the problem (parents actually doing the kind of work I ask students to do!)
  • Sharing our methods for solving the problem
  • Drawing conclusions about the thinking that was taking place
  • Rethinking philosophy about the teaching and learning of mathematics: why it is better to really think in math class and not just do pages of (usually) meaningless problems
  • Questions and Answers

Parents just want what is best for their children, and we want to help parents understand something about mathematics curriculum, and in so doing, grasp a vision of deeper mathematical understanding for their children.

I’d love to hear from you if you host your own event!

Mathematically yours,

Carollee

Use What You Know to Figure Out What You Don’t Know March 7, 2014

I was working with some students this week who were learning their “basic facts” in multiplication. These are generally considered to be those one-digit times one-digit problems that we use when we figure out the products of multi-digit problems. I was going over some different strategies and ways of thinking that can be used to help students learn those facts.

There are a number of strategies that can help in the learning of basic facts, but one phrase sums up many of those individual strategies: “Use what you know to figure out what you don’t know.”

This phrase actually applies to FAR more than just the learning of basic facts. The truth, however, is that often we condition students to NOT think for themselves in mathematics. We have a long tradition of teaching by telling: the “here’s how to do it now go practice 50” method. In reality, that kind of math lesson programs students to think that unless someone has told them “the way” to do something (and, of course, they must remember exactly how to follow the directions of “the way”). If they forget, they are stymied and cannot know how to proceed. They remain in their “stuck” position until someone comes to rescue them with “the way”.

It is far better to regularly encourage students with the idea that when they are stuck, they need to stop and think about the things they DO know that can be applied. We might ask questions (and teach them to ask themselves) such as these:

• What might be something similar that you do know?
• If the problem had smaller or simpler numbers, how would you try to solve it?
• Why did you choose to do it that way?
• What is important in the question?
• Is there a pattern?
• Is there a way to record what you have done so far so you a pattern might be noticed?
• Can you think of another way to do that?
• Does this remind you of another problem you have done?

In the case of basic facts, “Use what you know to figure out what you don’t know,” might look like this: a student cannot remember 6 x 8. But 5 x 8 is known. So, knowing that 5 groups of 8 is 40, he need only add one more group of 8 to have the needed 6 groups of 8; thus 40 + 8 = 48 is the solution to the unknown fact.

Students may need practice in doing such strategies, but the important thing is that there ARE strategies to help. It removes the case of having to rely solely on memory and sitting there stuck if memory fails.

What are you doing in your classroom today that encourages students to help themselves when they are stuck? Maybe post the title phrase for them (and model for them how it looks): “Use what you know to figure out what you don’t know.”

Strategies make a difference in student learning!

Mathematically yours,

Carollee

 

Number of the Day – Level II March 6, 2014

In keeping with my belief that elementary school that students should be involved with numbers everyday in math time, I am posting my Number of the Day Level II sheet in English and French.

Today’s sheet is one to use primarily with numbers to 30. As in the Level I sheet, most of the components are self explanatory, and again the colouring on the 100 chart can be done either by colouring the individual number or by colouring all numbers up to and including the number of the day.

As mentioned before, breaking the number apart in different ways is an import thing for students to practice. As John Van de Walle wrote, “To conceptualize a number as being made up of two or more parts is the most important relationship that can be developed about numbers.” [Van de Walle, J. and Folk, S. (2005). Elementary and Middle School Mathematics: Teaching Developmentally (Canadian Edition). Pearson: Toronto.]

I am delighted to offer this sheet in a French version, as well. Merci to my friend and colleague Lynn St. Louis for her translation.

Download the English version here.

Download the French version here.

I’d LOVE to hear from you if you try either version!

Mathematically yours,

Carollee

Number of the Day – Level I March 5, 2014

I have long believed that in elementary school that students should be involved with numbers everyday in math time. This may not always be the case — the teacher might be teaching a unit on pattering or geometry, for instance. While those are worthwhile concepts, I still remain convinced that students need some time each day to think about and work with numbers.

One way this can be accomplished is through the use of Number of the Day sheets. The idea of using such a sheet is not new – indeed, there are many versions available on the Internet.

I have added my own version of the Number of the Day sheet into the mix. In fact, I will be adding several versions over the next few days that are targeted at different levels of learners

The Number of the Day sheet I am posting today is one that can be used in Kindergarten classes, but it may be useful in Grade one classes early in the school year. The components are self-explanatory, although I did have one teacher who started using the sheet call me and ask about colouring on the 25 chart. She asked, “If the number of the day is 12, am I supposed to have students just find and colour the numeral 12, or are they supposed to colour all the boxes up to and including 12?” My response was, “Yes!” Either way is good, with each method focusing on something slightly different about the number 12.

Breaking the number apart in different ways is an import thing for students to practice. As John Van de Walle wrote, “To conceptualize a number as being made up of two or more parts is the most important relationship that can be developed about numbers.” [Van de Walle, J. and Folk, S. (2005). Elementary and Middle School Mathematics: Teaching Developmentally (Canadian Edition). Pearson: Toronto.]

I am delighted to offer the sheet in a French version as well. Merci to my friend and colleague Lynn St. Louis for her translation.

Download the English version here.

Download the French version here.

Mathematically yours,

Carollee